During last year Advent of Code, I ended up discovering a beautiful relation between bounded integer compositions and the generalized Fibonacci sequence. Probably it is an already known relation, but the fact that it popped up in a totally unrelated problem is a remarkable example on how number theory properties may pop up in the most unexpected places.

As we have said before, skill and ranking are never measured directly; instead, they are inferred from the observed performance of a player in previous matches. The idea of building an estimator based on pairwise wins and losses is quite old, but the Elo System represents the most simple and popular implementation.

A Ranking Systems is a core element of every competitive game. Every game in which a player plays against another player need to have some way to rank them and compare the relative skill of each other. It happens for video games, but also sport (e.g., the FIFA ranking for football) or other games (e.g., FIDE Chess Ranking). Comparing stuff is in the human nature.

Because I started a small series about astronomical algorithms and the magic of math in space, I think we need to cover an important prerequisite. In the series, I will talk a lot about ellipses (duh), I will move from the semi-axis majors, to the periapsis, to eccentricity, to ellipse’s center and ellipse’s foci. I am concerned that things can get more complicated than expected if the readers does not know many of the geometric properties of the ellipse. For this reason, I put here this vade mecum on the ellipse geometry. A summary with all the basic points and lengths. A place that I can link everywhere I need to refresh a definition.

As you probably know, I am working (slowly) on an astronomically accurate calendar generator. All the orbital calculations involved are quite challenging, and I am discovering a lot. It is a lot of fun (except for the all the times I need to do some trigonometric magic to make some formula work). Anyway, during this process, I am reshaping and producing many many formulas. I am sure that in six months I will forget all the motivations behind them. For this reason, I want to try to save some of them here. In this way, I will have a good place where to look back at my notes and, moreover, I can be useful to other people trying to do some low-accuracy orbital calculations. I want to start from the beginning: orbital period and orbital trajectory.

Times ago, I was reading something on numerical systems and password generators and I find myself discovering Diceware, a system for generating a passphrase using several 6-side dice. I think it was funny, so I looked for some dice in my house to try the system. Unfortunately, I have just one d6. Diceware requires five throws just for a single word and a good passphrase requires 3 or 4 words, plus some modifiers here and there. In total, I should throw that single die 20 times to get a good passphrase.

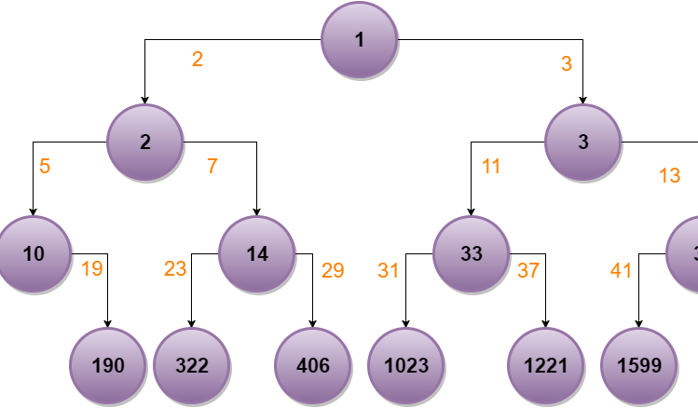
This will be just a small theoretical article on the Primes Ancestor Tree. We will explore the possibility to label a generic tree in such way that it will be possible to verify if a node is an ancestor of another node (or to find the common ancestor of two nodes) just by applying integer arithmetic.

In fact, sometimes ago I was trying to implement some fancy algorithm that, given two nodes from the open list of a search algorithm, finds their common ancestor. While I was doing this I asked myself if it was possible to use prime numbers in order to provide a labeling system that encodes the “descendant” relation of the nodes.

I think that I have found a theoretical system. Even if it can not be used in real-world applications, I had fun playing with it looking for the properties of the resulting labeled tree. So, I thought it could be interesting to share.