Che cos’è l’apprendimento? La domanda apre orizzonti molto complessi molti dei quali sono attualmente “zona di confine” e oggetto di numerose ricerche. Tuttavia possiamo iniziare a capire l’essenza intima dell’apprendimento tramite un piccolo gioco.
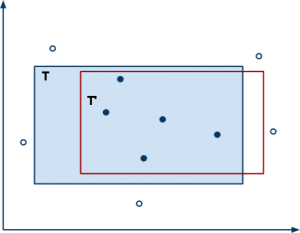
Supponiamo che ci vengano restituiti in modo casuale dei punti su di un piano cartesiano. Per ogni punto ci viene inoltre detto se si trova all’interno o all’esterno di un rettangolo disegnato sullo stesso piano ma di cui non conosciamo dimensione e posizione. Il gioco consiste nel tracciare il rettangolo che più si avvicina al rettangolo da indovinare con il minor numero di indizi. Nella figura seguente consideriamo i punti esterni come cerchietti bianchi e i punti interni come puntini neri.
Per questioni di semplicità consideriamo il rettangolo da cercare con i lati paralleli alle assi del piano cartesiano.
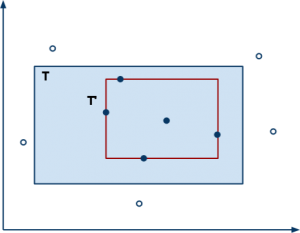
Una regola di ragionamento molto severa che possiamo applicare al seguente problema può essere la seguente. Ad ogni punto che ci viene dato consideriamo solo quelli interni, dopodiché tracciamo il più piccolo rettangolo allineato che contiene tutti i punti interni. Questo può essere fatto velocemente prendendo la massima (e la minima) coordinata X e la massima (e la minima) coordinata Y dell’insieme dei punti esterni. Questi 4 valori corrispondono alle posizioni dei segmenti che compongono il rettangolo.
Questo metodo ci fornisce subito un vantaggio. Il rettangolo che tracceremo sarà sempre interno al rettangolo reale, sarà sempre un approssimazione per difetto del rettangolo originale. Un sistema automatico così progettato apprenderà la forma e la posizione del rettangolo in modo autonomo basandosi solamente sull’input.
Come può questo esempio farci capire qualcosa sull’apprendimento? Se prendiamo l’esempio così com’è probabilmente nulla, ma se proviamo a sostituire l’asse delle X con “altezza” e quella delle Y con “peso” possiamo subito intuire che il rettangolo T potrebbe essere, ad esempio, l’insieme delle persone con peso-forma ideale. Un sistema che prova ad indovinare il rettangolo esatto tramite i vari indizi nel modo appena descritto apprenderà la classe “persone con peso forma ideale”.
Possiamo quindi iniziare a dare delle definizioni formali degli elementi che abbiamo presentato.
Il piano cartesiano prende il nome di contesto o spazio delle istanze. Nel caso generico tale spazio non è detto sia infinito ma potrebbe essere a sua volta un insieme di punti (ad esempio, nel caso del peso-forma, possiamo escludere i pesi superiori a 400 e inferiori allo 0, idem per le altezze ottenendo un contesto di forma rettangolare). Un contesto può anche avere dimensioni superiori alle due del piano, anzi, questo è solitamente il caso più frequente in quanto i vettori di parametri in ingresso spesso sono molto grandi.
Un concetto c nel contesto X rappresenta un qualunque sotto-insieme di X. Nel nostro caso tale concetto era rappresentato dal rettangolo T. In esempi alternativi un concetto potrebbe essere “tutte le matrici di pixel che rappresentano la lettera A” oppure “gli animali simili ad un gatto”. I concetti non è detto che siano rettangoli ma possono avere una forma qualsiasi all’interno del contesto. Una classe di concetti rappresenta un insieme di concetti nel contesto che definiscono una proprietà del concetto stesso. Nel nostro esempio una classe può essere “tutti i rettangoli allineati agli assi” in modo tale da escludere qualunque altra forma rettangolare e non allineata.
Infine ci sono due concetti importanti: il concetto obiettivo e il concetto ipotetico che nel nostro disegno sono rispettivamente T e T’. Il concetto obiettivo è la rappresentazione ideale di ciò che cerchiamo di apprendere mentre il concetto ipotetico è la versione nella nostra mente, o in quella di un calcolatore, ed è quella su cui basiamo le nostre decisioni.
Tutti questi elementi sono sufficienti a descrivere il processo dell’apprendimento nella sua interezza, sia esso di un uomo o di un automa. Gran parte dell’apprendimento, anche nel caso umano, ricalca queste definizioni. Fin da bambini infatti l’apprendimento consiste, almeno nella sua essenza, nel suddividere e associare i vari elementi del mondo reale (che possono essere oggetti fisici, emozioni oppure azioni e/o gruppi di azioni) all’interno di classi. Impariamo così a distinguere un gatto da una sedia, un’auto da una moto, un gesto utile da uno inutile e così via. La complicazione maggiore nel caso reale consiste nel vastissimo numero di parametri che vengono utilizzati per effettuare queste suddivisioni: forma, colore, odore, tipo di movimento, calore, periodo del giorno in cui l’oggetto appare, stato emotivo e molto altro. Senza parlare del fatto che molti parametri sono ancora poco quantificabili (vedasi il concetto di forma), oppure altri derivano a loro volta da classificazioni primitive (moto e auto si differenziano dal numero di ruote, ma cosa distingue una ruota da copertone poggiato ad un edicola?). E il tutto deve essere fatto in un tempo sufficientemente breve da essere “real-time” o quasi.
Inoltre il processo di aggiornamento di un concetto (apprendimento) è eseguito fondamentalmente in due modi: per rafforzamento e per emulazione.
L’apprendimento per rafforzamento è esattamente quello che succede nel gioco del rettangolo. Un essere umano (o una macchina) ricevono vettori di input e uno stimolo (che rappresenta la correttezza o la scorrettezza di un associazione). Se un bambino guarda l’acqua riceve in ingresso una nuvola di dati, se la sua classificazione è errata (ad esempio dice “pane” ma indicando l’acqua) la madre subito corregge dicendo “acqua” inviando un segnale demolitore (cerchio esterno), in caso contrario la madre sorriderà e porgerà l’acqua inviando un segnale rafforzatore (cerchio interno).
L’apprendimento per emulazione/induzione consiste invece nell’aggiornamento immediato del nostro “rettangolo” basandoci su quello di un altro. Tale procedimento non necessita necessariamente di prove concrete e segnali personali ma adattamenti basati su “quello che ci mostra un altro”. Ad esempio nessuno è andato mai a controllare che sulla Luna non ci sia aria personalmente eppure il nostro “rettangolo” delle “luoghi senza aria” comprende sicuramente la Luna. Ma essendo questo un comportamento quasi esclusivamente umano (gli animali non apprendono mai per emulazione) non mi dilungherò su esso.
Un altro punto fondamentale consiste nel fattore di sfumatura del contorno. Non sempre i concetti o le classi sono delimitate nettamente da un contorno, molto più spesso tale confine è sfumato. Qual è, ad esempio, la zona di confine che delimita la classe delle sedie da quella degli sgabelli? Qual è la linea di demarcazione fra calvi e non calvi? Tutte queste domande hanno una soluzione ovvia soltanto per punti molto interni o molto esterni al “confine”. Per punti prossimi allo stesso la situazione è più complicata, ci troviamo in una zona in cui si passa gradualmente da un concetto ad un altro o addirittura sono equiprobabili. Inoltre non potremmo nemmeno utilizzare segnali tanto chiari come “dentro” e “fuori” perché per i punti sul confine dovremmo quantificare quanto sia dentro e quanto sia fuori.
Il problema è che effettuare ragionamenti automatici con questo genere di insiemi è ancora pesantemente oggetto di studio. Non esiste, infatti, nessuna versione “probabilistica” o “fuzzy” della logica del primo ordine e successive, aree di logica strettamente collegate ai concetti di cui abbiamo appena parlato. La discussione su questo quindi può essere solo che rinviata alle prossime scoperte (al più presto speriamo).
La cosa importante però è che aggiungere un tale comportamento darebbe agli “automi” un comportamento molto umano: il dubbio. Il dubbio e l’incertezza umana è proprio data dal nostro percorre queste zone di confine che in concetti reali sono molte più di quelle che si riescano a valutare negli asettici laboratori di intelligenza artificiale.
Il dubbio è però anche quella cosa che ci spinge a cercare ulteriori informazioni per poter ridisegnare il nostro “rettangolo” in modo più preciso. Cartesio diceva: “Dubito ergo cogito ergo sum”. Chissà che presto non siano anche gli automi a dubitare e quindi a “essere” qualcosa di più.

 Follow
Follow
Come te, auspico che le ricerche in questo ambito portino, un giorno, speriamo il più vicino possibile, ad un automa in grado di avere quei tratti caratteristici degli umani che fin’ora non siamo riusciti a ricreare.
Creo che questo “giocare a fare Dio”, ci porterà ad avere una conoscenza più profonda di noi stessi e delle leggi che regolano la nostra esistenza.
Bellissimo articolo, hai centrato nel modo più chiaro e coinciso possibile i traguardi presenti e futuri delle neuroscienze 😉
Sto cominciando a leggere quel libro che ti avevo linkato. Infatti l’esempio del rettangolo e la terminologia tecnica l’ho presa da li.
E’ abbastanza complicato infatti sto andando lento, ma è molto illuminante. 🙂