Luna Lander: Simulazione

Nella maggior parte della applicazioni grafiche la simulazione di comportamenti fisici ricopre un ruolo fondamentale. Per questo motivo vi farò vedere un metodo piuttosto elementare ed efficiente per simulare una navicella sottoposta ad un campo gravitazionale costante. Se conoscete il gioco Luna Lander avete già capito a cosa voglio arrivare.

Analisi Fisica

Il primo passo di ogni simulazione fisica consiste nello studiare nel modo più preciso possibile qual’è il comportamento fisico degli oggetti da simulare. Nel nostro caso l’unico elemento che ci interessa è la navicella.

Dal disegno vediamo che in un generico momento la nostra navicella è sottoposta ad una forza F orientata di $\theta$ lungo l’asse verticale. La forza F rappresenta infatti la forza generata dal motore della navicella orientata sempre lungo l’asse della navicella.

Usando la classica formula della dinamica otteniamo:

$m a_x = F sin(\theta)$
$m a_y = F cos(\theta) - m g$

Dividendo tutto per la massa della navicella:

$a_x = \frac{F}{m} sin(\theta)$
$a_y = \frac{F}{m} cos(\theta) - g$

Il nostro sistema ora è completamente descritto. Tuttavia in questa forma differenziale non è ancora sfruttabile dalla nostra applicazione.

Individuare gli ingressi

Il secondo passo consiste nell’individuare gli ingressi ovvero cosa dipende dallo stato e cosa dipende dall’input? Questo è importante perché gli ingressi sono del tutto imprevedibili o perché troppo complessi da predirre oppure perché generati dal libero arbitrio del giocatore. Nel nostro caso il giocatore controlla direttamente due parametri:

La forza F del motore. Premendo un tasto (ad esempio la freccetta su) il motore è acceso e genera una forza F, quando il tasto non è premuto il motore è spento e la forza generata è pari a zero.
L’angolo $\theta$ con cui è orientata la navicella. Per semplicità assumiamo che solo tre valori siano possibili e che tali valori cambino istantaneamente alla pressione del tasto corrispondente. Premendo il tasto direzionale destro $\theta = \frac{\pi}{4}$ , premendo il tasto sinistro $\theta = - \frac{\pi}{4}$ e non premendo nulla $\theta = 0$ .

Integriamo

A questo punto, dalla legge che descrive l’accelerazione dobbiamo ricavare la funzione che descrive la posizione (che ci interessa sapere per disegnare la nave sullo schermo nel punto giusto).

Tuttavia integrare una funzione del genere analiticamente è impossibile. Come fare? Approssimando. A questo punto molti metodi sono stati sviluppati ma qui di seguito vi presento il metodo che ho usato più spesso per questo genere di cose. Non so se sia il più preciso ma offre un ottimo realismo con prezzi computazionali piuttosto irrisori.

L’idea che sta alla base di questo metodo è di considerare gli ingressi dell’utente come costanti (sebbene varino platealmente con il tempo). In questo modo integrare $a_x$ e $a_y$ risulta un compito banale.

$v_{x}(t) = v_{x0} + a_x(t) t$
$v_{y}(t) = v_{y0} + a_y(t) t$

Da cui

$x(t) = x_0 + t v_{x0} + \frac{1}{2} a_x(t) t^2$
$y(t) = y_0 + t v_{y0} + \frac{1}{2} a_y(t) t^2$

Discretizziamo

Con una formula in tempo continuo ci facciamo ancora poco. Il computer lavora per cicli e, per quanto questi cicli possano essere piccoli, non possono certo essere considerati continui. Per far questo discretizziamo. Un metodo molto semplice consiste nel sostituire $t = \gamma k$ . Dove $k$ assume solo valori interi e $\gamma$ rappresenta la dimensione degli intervalli del ciclo (per simulazioni realtime $\gamma$ viene scelto pari a $\frac{1}{fps}$

La formula riscritta in questo modo assume la forma:

$v_{x}(k) = v_{x0} + a_x(k) \gamma k$
$v_{y}(k) = v_{y0} + a_y(k) \gamma k$
$x(k) = x_0 + \gamma k v_{x0} + \frac{1}{2} a_x(k) \gamma^2 k^2$
$y(k) = y_0 + \gamma k v_{y0} + \frac{1}{2} a_y(k) \gamma^2 k^2$

Calcoliamo una formula incrementale

La formula precedente ha un grande svantaggio. Ci costringe a dover mantenere nella memoria la velocità iniziale, la posizione iniziale e il numero di cicli trascorsi dall’inizio della simulazione. Senza contare che questa formula da valori completamente sbagliati perché assume che l’accelerazione sia sempre costante: in questo modo quando l’utente accenderà il motore la formula ci darà la posizione che avrebbe avuto la navicella se il motore fosse sempre stato acceso dall’inizio, e viceversa, e non il valore corrispondente ad un motore appena acceso!

Ma a questo c’è una soluzione: basta trovare una formula incrementale che condensi tutte queste informazioni nel suo stato passato.

Per prima cosa vediamo la velocità. Calcoliamo la velocità per $\latex k+1$.

$v_{x}(k+1) = v_{x0} + a_x(k) \gamma k + a_x(k) \gamma$
$v_{y}(k+1) = v_{y0} + a_y(k) \gamma k + a_y(k) \gamma$

Bene. Possiamo subito notare che questa formula è equivalente a:

$v_{x}(k+1) = v_{x}(k) + a_x(k) \gamma$
$v_{y}(k+1) = v_{y}(k) + a_y(k) \gamma$

Con un procedimento analogo possiamo ricavare anche

$x(k+1) =x(k) + \gamma v_{x}(k) + \frac{1}{2} \gamma^2 a_x(k)$
$y(k+1) =y(k) + \gamma v_{y}(k) + \frac{1}{2} \gamma^2 a_y(k)$

Ora abbiamo una formula iterativa che ci permette di calcolare il moto della navicella sotto il comando dell’utente. Possiamo riassiumere l’algoritmo finale in questo modo:

Per ogni “frame” facciamo

Tramite i comandi dell’utente calcoliamo $a_x$ e $a_y$ .
Usando i valori appena calcolati e i valori di x, y e velocità precedenti calcoliamo i nuovi valori per x, y e v.

Rendere coerenti le unità di misura e i sistemi di riferimento

Tutto il nostro ragionamento è fatto sulla base di unità di misure fisiche (metri su secondo). Lo schermo però si comporta diversamente. Le coordinate di un oggetto sullo schermo, ad esempio, sono quasi sempre indicate in pixel e non i metri. Dobbiamo quindi scalare i dati di x e y in modo tale che siano coerenti con la rappresentazione grafica.

Se ad esempio un metro sullo schermo ha una dimensione di 10px dobbiamo moltiplicare il valore di x e y di un fattore 10. Analogamente facciamo l’opposto se un pixel rappresenta 10 metri. 🙂

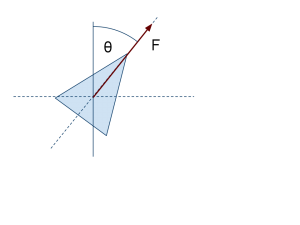
3 comments on “Luna Lander: Simulazione”

md1512 on June 7, 2011 at 20:51 said:

Mi potresti farmi venir voglia di studiare per l’esame di fisica.
- THeK3nger on June 8, 2011 at 10:51 said:
  
  Se nei corsi di fisica facessero vedere qualche bella applicazione pratica della stessa sarebbero più appassionanti 😉
- Anonymous on June 21, 2011 at 14:52 said:
  
  Se nei corsi di fisica facessero vedere qualche bella applicazione pratica della stessa sarebbero più appassionanti