Follow

Dopo aver visto come funziona la ricorsione in Scheme dobbiamo valutare un altro aspetto molto rilevante: il costo. Non tutto ciò che logicamente funziona funziona poi all’atto pratico. Ad esempio, se ripescate la funzione ricorsiva della Funzione di Fibonacci e provate a farla partire noterete che già con numeri relativamente bassi (come 100) il sistema inizierà a intasarsi e non darà alcun risultato se non quello di dover killare il processo.

Perché questo? Perché l’implementazione dell’algoritmo, sebbene sia vera e matematicamente corretta, necessita un numero troppo elevato di calcoli o di memoria.

Iniziamo col dare dei cenni sulla complessità di un algoritmo. La complessità di un algoritmo è definita asintoticamente con un infinito di ordine superiore a una funzione f(x). In questo caso si dice che l’algoritmo ha complessità dell’ordine di f(x).

Cosa significa? E’ semplice. Supponete di far valere 1 il costo di ogni operazione base come somma, prodotto, cdr, car e via dicendo (ovviamente è un approssimazione). Supponete di stabilire un contatore che sommi il costo di ogni operazione eseguita. Supponete poi di eseguire questa funzione (con relativo contatore) per un imput di dimensione 1, poi per un input di dimensione 2, poi per un input di dimensione 3 e così via. La serie di numeri che otterrete non sarà altro che i valori di una funzione f(x)al variare di x. La complessità si riduce quindi all’ordine di infinito di questa funzione.

Data l’asintoticità della definizione, solitamente si trascurano i valori per x piccolo e si approssima molto per x che tende a infinito.

Senza addentrarci nei particolari sappiate che in ogni algoritmo esiste un operazione, detta operazione dominante, la quale complessità è uguale alla complessità dell’algoritmo nella sua interezza.

Negli algoritmi ricorsivi l’operazione dominante è la ricorsione. Per trovare la complessità di una funzione in scheme (che sono per definizione tutte ricorsive) ci basta quindi sapere quante volte una funzione chiama la ricorsione.

Questo può essere molto complicato, ma è giusto che impariate a identificare almento i casi semplici. Questo può essere fatto molto semplicemente.

Supponiamo di voler calcolare la complessità dell’algoritmo fattoriale visto qualche lezione fa. L’espressione ricorsiva del fattoriale è la seguente:

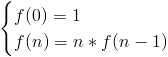Per trovare il costo basta seguire la formula:

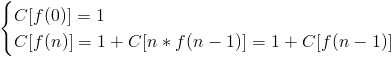Questo perché il costo di f(0) è chiaramente unitario. Il costo di f(n), per il principio dell’operazione è solamente il costo della ricorsione e il costo della ricorsione non è altro che 1 più il costo di tutte le altre funzioni invocate.

Ma siamo arrivati ad una suluzione? Ancora no. Dobbiamo esplicitare il costo ovvero toglierlo dalla sua forma ricorsiva. Per fare ciò possiamo semplicemente espandere la seconda equazione.

• C[f(n)]
• 1 + C[f(n-1)]
• 2 + C[f(n-2)
• …
• n + C[f(0)]
• n+1
• che è asintoticamente O(n)

Il costo è quindi lineare. (Non esattamente… ma per non mettere troppa carne al fuoco farò alcune precisazioni al riguardio nella prossima appendice).

Una funzione con complessità lineare è solitamente una funzione discretamente veloce e potente.

Vediamo ora la stessa cosa con la Funzione di Fibonacci.

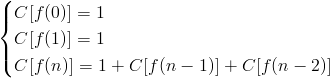
La situazione è leggermente più complessa. Per esplicitare la funzione possiamo comunque espandere C[f(n)] ma non conviene in questo caso. Facciamo un ragionamento più sottile. Cerchiamo di calcolare direttamente il costo totale. Sappiamo che ogni ricorsione chiama due ricorsioni. Alla prima ricorsione avremo costo totale 1, alla seconda avremo il costo totale di prima più il costo delle due nuove ricorsioni ovvero 1 + 2. Alla terza avremo il costo di prima  più le due ricorsioni nuove lanciate da ognuna delle due ricorsione precedenti ovvero 1 + 2 + 4 (il costo di prima più le due ricorsioni nuove lanciate da ognuna delle due ricorsione precedenti).

Notiamo che abbiamo una serie geometrica che possiamo riassumere in 2^n+1 – 1 che asintoticamente è O(2^n).

Il costo è esponenziale. Un algoritmo esponenziale può solitamente calcolare solo input molto piccoli. Ecco perché il nostro algoritmo di Fibonacci si bloccava anche con numeri piccoli come 100.

Come possiamo allora migliorare questo algoritmo? Esistono tecniche un po’ più elaborate che permettono di eseguire algoritmi simili lanciando solo una ricorsione al posto delle due “canoniche”. Queste tecniche le esploreremo più in là in quanto necessitano di un po’ di esperienza.

Per il momento vi basti intuire che algoritmi che eseguono troppe ricorsioni contemporaneamente sono spesso troppo costosi per essere utili. Infatti abbiamo visto che basta lanciare due ricorsioni in vece di una per fare esplodere il costo da lineare ad esponenziale.

Non vi serve saper calcolare la complessità di tutto ma vi basta intuire quando un algoritmo sta diventando troppo costoso. Questo è basilare per ogni programmatore, anche al di là di Scheme.

Provate a calcolare il costo di altre funzioni di esempio che ho dato in precedenza. Postate il costo che avete ottenuto nei commenti e vedrò di verificare se avete indovinato.